Med tanke på att binär är så helt grundläggande för att det finns datorer, verkar det konstigt att vi aldrig har tagit upp ämnet tidigare - så idag tänkte jag att jag skulle ge en kort översikt över vad binärt egentligen betyder och hur det används i datorer . Om du alltid har undrat vad skillnaden är mellan 8-bitars, 32-bitars och 64-bitars verkligen, och varför det spelar roll - läs sedan vidare!
Vad är binärt? Skillnaden mellan bas 10 och bas 2
De flesta av oss har vuxit upp i en bas 10 värld av siffror, vilket betyder att vi har 10 "bas" nummer ( 0-9 ) från vilka vi härleder alla andra nummer. När vi har uttömt dem flyttar vi upp enhetsnivå - 10, 100, 1000-talet - denna form av räkning hamras i våra hjärnor från födseln. Det var faktiskt bara från den romerska perioden som vi började räkna i bas 10. Innan det var bas 12 det enklaste, och folk använde sina knogar att räkna.
När vi lär oss bas 10 i grundskolan skriver vi ofta ut enheterna så här:
Så numret 1990 består faktiskt av 1 x 1000, 9 x 100, 9 x 10 och 0 x 1 . Jag är säker på att jag inte behöver förklara bas 10 längre än det.
Men vad händer om istället för att ha ett helt urval av 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 för att arbeta med som basnumren - vad händer om vi bara hade 0 och 1 . Detta kallas bas 2 ; och det är också vanligtvis kallat binärt . I en binär värld kan du bara räkna 0, 1 - då måste du flytta till nästa enhetsnivå.
Räkna i binär
Det hjälper oerhört om vi skriver ut enheterna när de lär sig binärt. I det här fallet, istället för att varje ytterligare enhet multipliceras med 10 multipliceras den med 2, vilket ger oss 1, 2, 4, 8, 16, 32, 64 ... Så för att hjälpa beräkna kan vi skriva ut så här:
Med andra ord representerar det högsta värdet i ett binärt tal hur många 1 är. Nästa siffra, till vänster om det, representerar hur många 2 s. Nästa representerar hur många 4: e ... och så.
Med den kunskapen kan vi skriva ut ett bord med räkning i binär, med motsvarande basvärde 10 som anges till vänster.
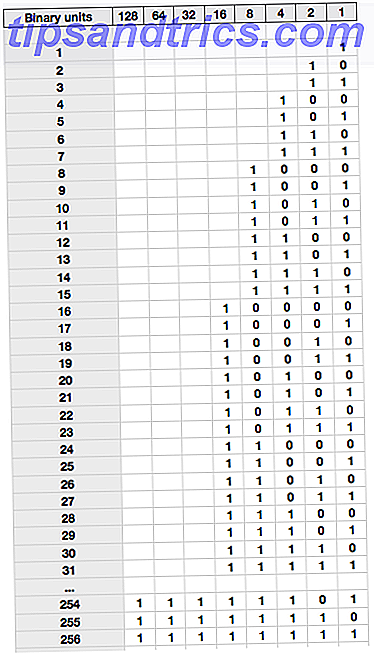
Tillbringa en stund över det tills du kan se exakt varför 25 är skrivet som 11001. Du borde kunna bryta ner den som 16 + 8 + 1 = 25.
Arbetar bakåt - bas 10 till binär
Du borde nu kunna räkna ut vad värde ett binärt tal har genom att dra en liknande tabell och multiplicera varje enhet. Att byta en vanlig bas 10 tal till binär tar lite mer ansträngning. Det första steget är att hitta den största binära enheten som "passar in" i numret. Så till exempel, om vi gjorde 35, så är det största antalet från det bordet som passar in i 35 32, så vi skulle ha en 1 där i den kolumnen. Vi har då en återstod av 3 - vilket skulle behöva en 2, och då äntligen en 1. Så vi får 100011 .
8 bitar, byte och oktetter
Tabellen jag har visat ovan är 8-bit, eftersom vi har högst 8 nollor och de som ska användas för vårt binära nummer. Således är det maximala antalet vi kan möjligen representera 11111111 eller 255 . Det är därför som vi behöver minst 8 bitar för att kunna representera ett tal från 0-255 . Octet och Byte är helt enkelt ett annat sätt att säga 8-bitars. Därför 1 Byte = 8 bitar .
32 vs 64-bitars dator
Numera hörs ofta villkoren 32-bitars och 64-bitars versioner av Windows, och du kanske vet att 32-bitars Windows bara kan stödja upp till 4 gigabyte RAM . Varför är det dock?
Allt kommer ner till minnesadressering. Varje bit av minne behöver en unik adress för att komma åt den. Om vi hade ett 8-bitars minnesadresseringssystem skulle vi bara kunna ha högst 256 byte minne. Med ett 32-bitars minnesadresseringssystem ( föreställ dig att du förlänger tabellen ovan för att ha 32 binärenhetskolonner ) kan vi gå någonstans upp till 4, 294, 967, 296 ? 4 miljarder bytes, eller med andra ord - 4 GIGA bytes. 64-bitars databehandling avlägsnar väsentligen denna gräns genom att ge oss upp till 18 quintillion olika adresser - ett nummer som de flesta av oss helt enkelt inte kan förstå.
IPv4-adressering
Den senaste oroen i datorvärlden handlar om IP-adresser IPv6 och kommande ARPAgeddon [Teknologi förklaras] IPv6 och kommande ARPAgeddon [Teknologi förklarad] Läs mer, särskilt IPv4- adresser, som dessa:
- 192.168.0.1
- 200.187.54.22
De består faktiskt av 4 nummer, var och en representerar ett värde upp till 255. Kan du gissa varför? Ja, hela adressen representeras av 4 oktetter (totalt 32 bitar ). Det verkade som en väldigt många möjliga adresser ( cirka 4 miljarder i själva verket ) när internet först uppfanns, men vi går snabbt ut nu när allt i vårt liv måste kopplas samman. För att lösa detta, använder den nya IPv6 128 bitar totalt, vilket ger oss cirka 340 undecillion ( sätt 38 nollor i slutet ) adresser att spela med.
Jag ska lämna den där för idag, så jag kan återvända till mitt ursprungliga syfte som skulle skriva nästa Arduino-handledning - där vi använder omfattande användningen av ett bitskiftregister. Jag hoppas idag har gett dig en grundläggande förståelse för hur binär är så signifikant för datorer, varför samma nummer förekommer, och varför antalet bitar vi måste representera någonting sätter en begränsad gräns för mängden minne, skärmstorlek, möjlig färg värden eller unika IP-adresser som är tillgängliga för oss. Nästa gång tar vi en titt på binära logiska beräkningar, vilket är ungefär vad en datorprocessor gör, liksom hur datorer kan representera negativa tal.
Kommentarer? Förvirring? Hittade du min förklaring lätt att förstå? Oavsett fall, var god kontakta oss i kommentarerna. Jag ska lämna dig med ett binärt skämt!
Det finns bara 10 typer människor i världen: de som förstår binära, och de som inte gör det.
Bildkredit: Shutterstock